Rugosity as a New Planning Paradigm

By Reid Ewing

Planning students in the 1970s all studied the monocentric city model. It is a descriptive model in which land uses form concentric rings around the city center, with different uses bidding for land and the highest and best use capturing the land in each ring. In this model, the city has one unique center, the central business district, with offices around it. The outer-most ring is low-density, single-family residential, with open space (agriculture) beyond that. The basic development of the monocentric model occurred in the 1960s and 1970s, largely through the work of William Alonso, Edwin Mills, and Richard Muth. Most urban economics courses still introduce students to the monocentric city model, so you have probably seen it before.

In the 1980s, planners, economists, and geographers began to note that larger metropolitan areas had developed a hierarchy of centers, and so hypothesized that polycentric development is a natural outcome of growth. Again, open space (agriculture) would occur at the fringe. Joel Garreau popularized this notion in Edge City: Life on the New Frontier, published in 1991. I wrote about the benefits of polycentric development in my May 2017 column.

A new article, "High Rugosity Cities: The Geographic, Economic and Regulatory Pathology of America's Most Non-Concentric Urban Areas," published in Land Use Policy by UC Davis Professor Catherine Brinkley, attempts to push this concept further. I have never featured Land Use Policy in this column. It is not a standard planning journal. But what could be more central to urban planning than land-use policy? For academic planners, Land Use Policy has an impact factor of 3.194, which puts it up there with the highest ranked planning journals.

I have also never featured rugosity in this column. The word isn't part of my vocab. It's defined as a measure of surface roughness and routinely used by coral reef biologists. Areas of high rugosity allow corals to attach and grow. The term is also used in medical sciences to approximate complex topographies. But what does it have to do with cities?

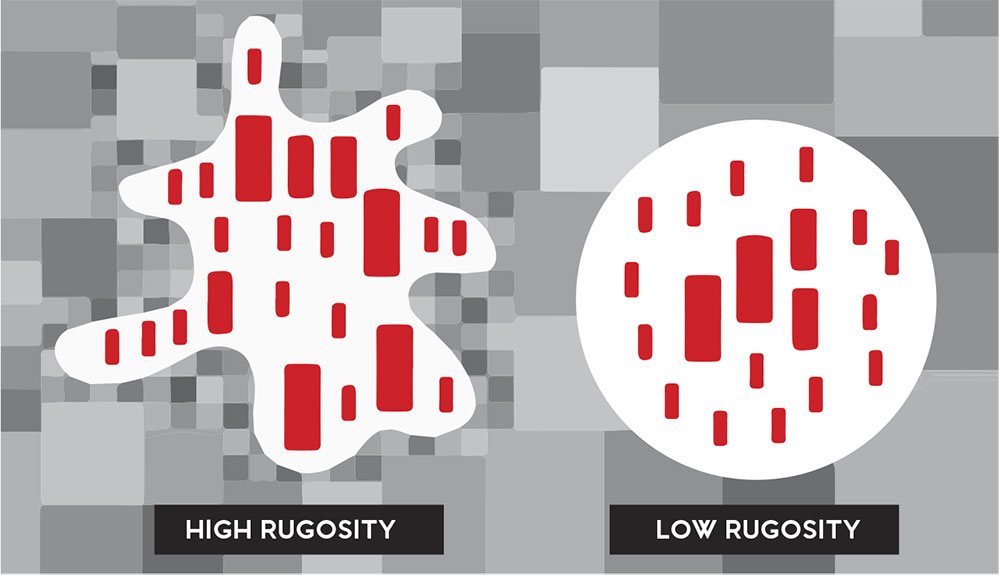
Differing rugosity for the same urban area compared to a non-urban area (in grayscale). Higher urban rugosity can be achieved by maximizing the urban interface through implementation of greenbelts, green wedges, and wildlife habitat corridors. Image by Nicole Martin.

Rugosity versus concentric growth

Brinkley explains it this way:

The guiding theory in urban development largely views nonconcentric urban form as undesirable and even pathologic. ... As a result, the dominant planning discourse calls for concentric urban areas, thereby minimizing the urban [-rural] interface. Yet, the urban interface is known to be important to housing markets, particularly where farmland amenities are valued. ... High-rugosity urban areas are associated with the sustained vigor of both urban and agricultural land uses.

She argues that cities should work more like coral reefs than concentric circles — supporting a diversity of niches and uses for sustained vigor and resilience. High urban rugosity can be achieved by maximizing greenbelts, green wedges, wildlife-habitat corridors, working lands such as ranches or farms, and park space.

To quantify rugosity, Brinkley uses GIS to measure the rural-urban interface in 483 counties. These counties are selected because they are part of metropolitan areas and have agricultural sales of over $50 million per year. The urban perimeter is measured for each county, and this in turn is used to compute a comparative rugosity index. The actual perimeter is divided by the perimeter of a concentric area encompassing the same amount of land to find the degree to which each urban area exhibits nonconcentric morphology.

The 30 counties with the most nonconcentric forms are selected for case study analysis. Many of the counties with the highest-rugosity scores are among the top agricultural producing counties in the U.S., far exceeding the $50 million floor for case study selection.

Threats to validity

The articles featured in this column often provide teachable moments, and this column is no exception. The Brinkley article contains a quantitative analysis that uses a series of development-related variables — including the urban population, population growth, housing stress, farmland acreage, community-supported agricultural sales, and 43 variables representing individual states (with so-called dummy variables, either zero or one) — to explain the urban area perimeter (miles of urban-rural interface) of each county.

Unfortunately, this analysis is compromised by the presence of a confounding variable: the population of the urban area, which is an extraneous variable correlated with other independent variables (such as community supported agricultural sales) and the dependent variable, the urban area perimeter. Large urban areas, measured in terms of population, have more of everything — coffee houses, pigeons, and, of course, miles of perimeter. As a result, the study's findings would be more meaningful if the dependent variable were a dimensionless measure of rugosity, such as the comparative rugosity index, defined above as actual miles of perimeter divided by the miles of perimeter in an identically sized concentric area. I would also drop the confounding variable of population size.

This analysis also presents the statistical issue of endogeneity. In a statistical model, you have an endogeneity problem when there is a correlation between your independent variable x and the error term in model e. In this case, y = a + b x + e.

Endogeneity most often arises when your independent variable x is a function of your dependent variable y, and vice versa. This condition is known as "reverse causality." Farmland acreage affects the urban perimeter, and the urban perimeter also affects farmland acreage, but it is unclear which is the cause and which is the effect. Community-supported agriculture arguably depends on both. Endogeneity biases regression coefficients.

To address endogeneity, I would approach this problem not with simple linear regression, but instead with structural equation modeling, discussed in a previous column.

Finally, the analysis may lead to false inferences of statistical significance because there are so many independent variables. The conventional significance level, 0.05, means there is a five percent chance a variable will incorrectly be labeled significant. With 48 variables, we would expect at least two false positives where variables are mislabeled.

Notwithstanding these methodological issues, Brinkley's article blazes a new trail in its challenge to the dominant theory in urban economics: the monocentric city model. As a measure of urban development, rugosity offers the best of both the monocentric- and the polycentric-city models because it is elegantly simple to calculate and use, but still encompasses the complexity of polycentric development. These are big advantages, and because of them, I could see many planning agencies working measures of rugosity into regional land-use plans in the very near future.

Reid Ewing is a distinguished professor of city and metropolitan planning at the University of Utah, an associate editor of the Journal of the American Planning Association, and an editorial board member of the Journal of Planning Education and Research, Landscape and Urban Planning, and Cities.